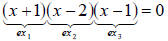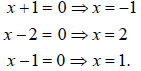|
|
Solving Equations I-Expressions Involving Power Functions
Toolbox—Combining Like Terms
Example 2.1 Simplify the expression (x +1)y + 4xy by combining like
terms.
We can deconstruct the left part of the sum into the product of x +1 and y. One
way to
deconstruct the right part of the sum is to split it into the product of 4x and
y. Using this
deconstruction, we see that y is a common term to each product, so (x +1)y and
4xy
are like terms. To combine them, we factor out the common term and add or
subtract
whatever is left over. Here the leftover pieces of the like terms are
expressions involving
variables themselves—not just numbers. So what!
 |
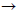 identify the common term,
identify the common term, |
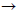 factor out the common term,
factor out the common term, |
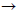 add the leftovers.
add the leftovers. |
Example 2.2 Simplify the expression
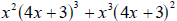 by combining like terms. by combining like terms.
This expression may not, at first glance, seem to have any like terms. But if
you look
back at Solution 2 of Example 1.3, both the left and right pieces of the sum
have a
common factor of 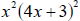 . We use the same method as
in the first two examples . We use the same method as
in the first two examples
above:
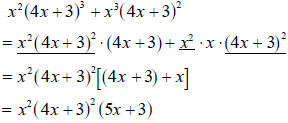 |
|
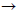 identify the common term,
identify the common term, |
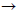 factor out the common term,
factor out the common term, |
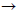 add the leftovers.
add the leftovers. |
Example 2.3 Simplify the expression
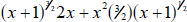 by combining like by combining like
terms.
We have to play with this expression a little bit to find out which
deconstruction will be
most useful to us. Right now you may be having trouble knowing the difference
between
what is useful and what is practically useless. What we optimally want is to
identify all
the common terms.
A useless way: Deconstruct the left-hand piece of the sum into the product of 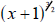 and
and
2x. Split the right hand piece of the sum into the product of
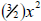 and and 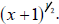 This This
deconstruction, though a perfectly legal (mathematically anyway) way to see the
expression, will not help us at all since we have not identified any common
terms in the
two products. Don’t give up—try again!
A useful way: Look at the left-hand piece of the sum as the product of x and
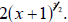
Turn the right hand part of the sum into the product of x and
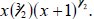 We have We have
now found one common term—the x—so this is a good start.
An even more useful way: Notice that the leftover terms in the previous way each
contain
the component x +1, but raised to different powers. Use this! Since
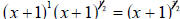 , we can turn the left-hand part of the sum
into the product of , we can turn the left-hand part of the sum
into the product of
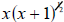 and 2(x +1). The right hand part of the sum
can be written as the product of and 2(x +1). The right hand part of the sum
can be written as the product of
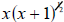 and and 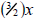 .
Thus we still see the common term of x, but also the common term .
Thus we still see the common term of x, but also the common term
of 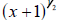 . .
We conclude the example by using this last deconstruction.
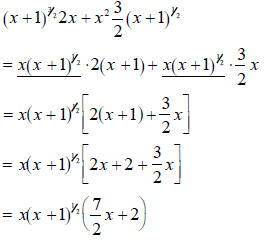 |
|
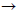 identify the
common term, identify the
common term, |
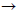 factor out
the common term, factor out
the common term, |
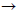 add the
leftovers. add the
leftovers. |
| |
Note. In the preceding example, we stopped identifying
common terms after we found
the common term 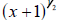 .
Could we have found any other common terms? How can .
Could we have found any other common terms? How can
you tell when you are done?
You can tell by looking at the leftover terms. In the example, 2(x +1) is
leftover from
the left-hand part of the sum, and
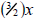 is leftover from the
right. Convince yourself that is leftover from the
right. Convince yourself that
these leftover terms cannot be split into products that have a common term.
Common Mistake. A common error here is to think that x is a common term to each,
and
that we could factor out the x from both 2(x +1) and
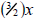 . But we cannot write . But we cannot write
2(x +1) as x · something. The ‘+1’ traps the x.
Toolbox—Zero Law
So what is the difference between an expression and an
equation? The simple answer is
that an equation has an ‘=’ symbol. This symbol sets up a relationship between
two
expressions—our goal is to find out where this relationship is true. What this
means is
that our job is to find out for which values of the variable is the left-hand
expression
equal to the right-hand expression.
The Zero Law is a way to turn more complex equations into two or more simpler
ones.
Let ex1 and ex2 represent expressions (like x +1 or x2 - 7x + 6). If
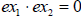 , for a , for a
particular value of x, then either that value of x makes
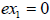 or it makes or it makes
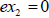 (or (or
possibly both). This is very helpful to us because looking for the solutions of
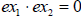 is the same as looking for the solutions of is the same as looking for the solutions of
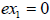 and and 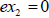 separately. Of
separately. Of
course we can do this with any number of expressions which are multiplied
together.
Note that the Zero Law only works if one side of the equation is already zero!
(Thus the
name…)
Example 2.4 Use the Zero Law to find the solutions of (x +1)(x - 2)(x -1) = 0.
The expression on the left side is the product of three expressions. The Zero
Law tells us
that finding which x make the left-hand side equal to zero is the same as
finding which x
make at least one of the three pieces on the left equal to zero. We have:
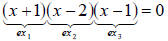
The Zero Law tells us we can solve instead the three
equations
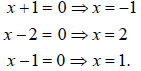
|


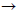 identify the common term,
identify the common term,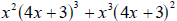 by combining like terms.
by combining like terms.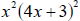 . We use the same method as
in the first two examples
. We use the same method as
in the first two examples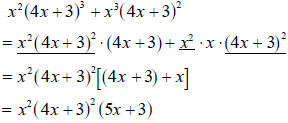
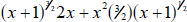 by combining like
by combining like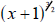 and
and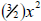 and
and 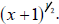 This
This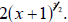
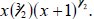 We have
We have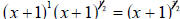 , we can turn the left-hand part of the sum
into the product of
, we can turn the left-hand part of the sum
into the product of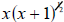 and 2(x +1). The right hand part of the sum
can be written as the product of
and 2(x +1). The right hand part of the sum
can be written as the product of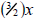 .
Thus we still see the common term of x, but also the common term
.
Thus we still see the common term of x, but also the common term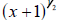 .
.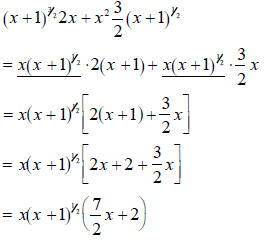
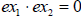 , for a
, for a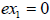 or it makes
or it makes
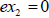 (or
(or